上 x(x^3-y^3) 3xy(x-y) solution 799089-X(x^3-y^3)+3xy(x-y) solution

X y = 3 3x y = 1 Solve by Substitution // Solve equation 2 for the variable y 2 y = 3x 1 // Plug this in for variable y in equation 1 1 (3x1) x = 3 1 2x = 4 // Solve equation 1 for the variable x 1 2x = 4 1 x = 2 // By now we know this much y = 3x1 x = 2 // Use the x If x and y are integers, then we can let y = x − k, where k is an integer Then the equation can be written as a quadratic in x k ( x 2 x ( x − k) ( x − k) 2) − x ( x − k) − 61 = 0 The solutions to this are x = k ( 3 k − 1) ± ( 1 − 3 k) ( k 3 k 2 − 244) 2 ( 3 k − 1) The term under the square root is only positiveSOLUTION 27x^3y^3z^39xyz (3x)^3y^3z^39xyz we have a identity That is (a^3b^3c^3)=(abc)(a^2b^2c^2abbccb)3abc From the above identity here a=3x b=y c=z expand according to identity ,we get (3xyz)(9x^2y^2z^23xyyzyz33xyz) (3xyz)(9x^2y^2z^23xy3xz3xz)33xyz9xyz (3xyz)(9x^2y^2z^23xy3xzyz)

Answered If U X Log Xy Where X3 Y3 3xy 1 Find Bartleby

X(x^3-y^3)+3xy(x-y) solution

X(x^3-y^3)+3xy(x-y) solution-Solution for 3xy (xy)= equation Simplifying 3xy (x y) = 0 (x * 3xy y * 3xy) = 0 Reorder the terms (3xy 2 3x 2 y) = 0 (3xy 2 3x 2 y) = 0 Solving 3xy 2 3x 2 y = 0 Solving for variable 'x' Factor out the Greatest Common Factor (GCF), '3xy' 3xy (y x) = 0 Ignore the factor 3 x^3 3x^2y 3xy^2y^3 (x y)^3 Solution Well you can use many methods to simplify like Using Pascal Triangle which give be 1, 3, 3, 1 as the expansion You can simplify (x y)^3 to either (x y) (x y) (x y) or (x y)^2 (x y) But using those two will result in same answer which will be in this format > 1, 3, 3, 1 Hence rArr (x y)^3 = (x y) (x y) (x y) (x y) (x y) (x

X 3 Y 3 Z 3 Novocom Top

(((x 3) (3x 2 • y)) 3xy 2) y 3 Step 3 Checking for a perfect cube 31 Factoring x 3 3x 2 y3xy 2 y 3 x 3 3x 2 y3xy 2 y 3 is a perfect cube which means it is the cube of another polynomial In our case, the cubic root of x 3 3x 2 y3xy 2 y 3 is xy Factorization is (xy) 3 Final result (x y) 3 `x^(3) y^(3) 1 3xy` का गुणनखंड ज्ञात कीजिये। `x^(3) y^(3) 1 3xy` का गुणनखंड ज्ञात कीजिये। Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Step by step solution by expertsMathx^3 /mathmath y^3/math = 3xy d/dx(mathx^3 /mathmath y^3/math) = d/dx(3xy) 3mathx^2/math 3mathy^2/math * dy/dx = 3y 3x * dy/dx 3mathx^2/math 3mathy^2/math * dy/dx 3mathx^2 /math 3x * dy/dx = 3y 3

1 Using the following fact the derivative of A B is the derivative of A the derivative of B you can split the problem into smaller parts Instead of trying to differentiate x 3 − 3 x y y 3 solve the three problems separately differentiate x 3 to get 3 x 2 (hint power rule d d x x n = n x n − 1)From Equation 3x 2 3y 2 30x72=0, we get y21=0 Y=±1 Solve the differential equation (3xy y^2 )dx (x^2xy ) dy=0 class 12 maths,Differential Equations by R B Gautam,class 12 maths differential equations impo

Changes made to your input should not affect the solution (1) "y3" was replaced by "y^3" 1 more similar replacement(s) Step 1 Equation at the end of step 1 (x•((x 3)(y 3)))3xy•(xy) Step 2 Trying to factor as a Difference of Cubes 21 Factoring x 3y 3 Theory A difference of two perfect cubes, a 3 b 3 can be factored intoThis problem has been solved!Solution Steps x ^ { 3 } 3 x ^ { 2 } y 3 x y ^ { 2 } y ^ { 3 } x 3 3 x 2 y 3 x y 2 y 3 Use the binomial cube formula, a^ {3}3a^ {2}b3ab^ {2}b^ {3}=\left (ab\right)^ {3}, where a=x and b=y Use the binomial cube formula, a 3 3 a 2 b 3 a b 2 b 3 = ( a b) 3, where a = x

Search Q X Y 5e3 Formula Tbm Isch

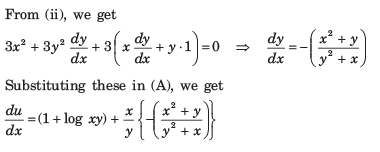
If U X Log Xy Wherex3 Y3 3xy 1 Then Du Dx Is Equal Toa B C D Correct Answer Is Option A Can You Explain This Answer Edurev Electronics And Communication Engineering Ece

Steps for Solving Linear Equation 3x4y=3 3 x − 4 y = 3 Add 4y to both sides Add 4 y to both sides 3x=34y 3 x = 3 4 y The equation is in standard form The equation is in standard formStep by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method xy=7;3xy=3 Tiger Algebra SolverFor xaxis to be the tangent of the curve x 3 y 3 = 3 x y, first you need to check if the curve intersects or touches with xaxis Since on xaxis y = 0 which should also satisfy x 3 y 3 = 3 x y Substituting y = 0, we obtain x 3 0 = 0 Which is satisfied for x = 0 Hence the curve touches or intersects with xaxis at (0, 0)

Answered Find The Following Derivatives Express Bartleby

Analyze The Product Of X 3 9y 3 3xy X Y

I think that 'find' would be a better word to use than 'solve' We'll start by dividing both sides of the equation by mathx^3/math, which gives us A math(1 \frac {y^3}{x^3Factor x y x y out of − x y 3 x y 3 Factor x y x y out of x y ( x 2) x y ( − 1 y 2) x y ( x 2) x y ( 1 y 2) Factor Tap for more steps Since both terms are perfect squares, factor using the difference of squares formula, a 2 − b 2 = ( a b) ( a − b) a 2 b 2 = ( a b) ( a b) where a = x a = x and b = y b = y(delf)/ (dely)=0` 3x 2 3y 2 30x72=0 and 6xy – 30y=0 ∴ y (6x30) =0 y=0, x= 5 For x=5;

X X3 Y3 3xy X Y Brainly In

If X 3 Y 3 3xy 2 3x 2y 1 0 Then At 0 1 Dy Dx

For the differential equation, x^2y" 3xy' 3y = x^3 (a) (Do Not Find the General Solution Use the transformation x = e^t, dy/dx = 1/x dy/dt and d^2y/dx^2 = 1/x^2 (d^2y/dt^2 dy/dt) to convert it to a 2nd order differential equation with constant coefficients) (Do Not Find the General Solution) (b) Find the general solution of x^2y" 3xy' 3y = x^3 using the method of Variation ofSolution for (y^33x^2y)dx (x^33xy^2)dy=0 equation Simplifying (y 3 3x 2 y) * dx 1 (x 3 3xy 2) * dy = 0 Reorder the terms (3x 2 y y 3) * dx 1 (x 3 3xy 2) * dy = 0 Reorder the terms for easier multiplication dx (3x 2 y y 3) 1 (x 3 3xy 2) * dy = 0 (3x 2 y * dx y 3 * dx) 1 (x 3 3xy 2) * dy = 0 Reorder the terms (dxy 3 3dx 3 y) 1 (x 3 3xy 2) * dy = 0 (dxy 3 3dx 3 y) 1 (x 3 3xySee the answer solve the equation (x9xy^4)dxe^x^2 y^3dy=0 An implicit solution in the form F (x,y)=C is = C

X Y 3 X3 Y3 3xy X Y Brainly In

Find Dy Dx By Implicit Differentiation X 2 Y 2 Chegg Com

Combine y^ {2}dx and xdy^ {2} to get 0 Combine y 2 d x and − x d y 2 to get 0 4ydx^ {3}=0 4 y d x 3 = 0 The equation is in standard form The equation is in standard form 4yx^ {3}d=0 4 y x 3 d = 0 Divide 0 by 4yx^ {3}This is a first order homogeneous differential equation, that is, the sum of the powers of x and y of each term multiplying dx and dy is constant, in this case 3 In this type, the substitution y = vx, dy = x*dv v*dx will always lead to a separation of the variables x and v The solution could be messyFactor x^3xy^2x^2yy^3 x3 − xy2 x2y − y3 x 3 x y 2 x 2 y y 3 Factor out the greatest common factor from each group Tap for more steps Group the first two terms and the last two terms ( x 3 − x y 2) x 2 y − y 3 ( x 3 x y 2) x 2 y y 3 Factor out the greatest common factor ( GCF) from each group

Factorise X3 9y3 3xy X Y Brainly In

X 3 Y 3 3xy 2 Find Dy Dx Using Implicit Differentiation Youtube

Solution for (x^23xyy^2)dxx^2dy=0 equation = 0 Factor a trinomial dx((y x)(y x)) = 0 Subproblem 1 Set the factor 'dx' equal to zero and attempt to solve Simplifying dx = 0 Solving dx = 0 Move all terms containing d to the left, all other terms to the right Simplifying dx = 0 The solution to this equation could not be determinedShow that f(x, y) = x3 y3 − 3xy 1 has a saddle point at (0, 0, 1) Students also viewed these mathematics questions P1042 Calculating and journalizing partialyear depreciationfurniture 3000 on December 3 and 4 16 respectively and that they were expected to last five years Assume that both assets have a residual value of 0 View Answer((x 3)(9•(y 3)))3xy•(xy) Step 2 Equation at the end of step 2 ((x 3) 3 2 y 3) 3xy • (x y) Step 3 Checking for a perfect cube 31 x 33x 2 y3xy 29y 3 is not a perfect cube Final result x 3 3x 2 y 3xy 2 9y 3

न म न व य जक क ग णनखण ड क ज य X X 3 Y 3 3xy X Y Youtube

How To Solve Math X 3 Y 3 Dx 3xy 2dy 0 Quora

Sinceif we put y=3/x in xy=3, we get x3/x =3 => (x^2 3)/x =3 => x^2 3x 3 =0 x comes out to be (3sqrt (3)*i)/2 and (3sqrt (3)*i)/2 Hence corresponding values of y are (3sqrt (3)*i)/2 and (3sqrt (3)*i)/2 In both cases, x and y are complex 555 views Cris Wellington , Math TeacherCalculus Find dy/dx x^3y^3=3xy^2 x3 y3 = 3xy2 x 3 y 3 = 3 x y 2 Differentiate both sides of the equation d dx (x3 y3) = d dx (3xy2) d d x ( x 3 y 3) = d d x ( 3 x y 2) Differentiate the left side of the equation Tap for more steps DifferentiateSimple and best practice solution for (xy^3y^2senx)dx= (3xy^22ycosx)dy equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it

Divide The Given Polynomials By Monomials X2y 3xy By Xy Snapsolve

Guaranteed Of Bonus If X 2 Y 3 3xy 2 1 Find Dy Dx In Terms Of X And Y Dy Dx Using Your Answer For Dy Dx Fill

2x35x2yxy26y3 Final result 2x3 5x2y xy2 6y3 Step by step solution Step 1 Equation at the end of step 1 (((2•(x3))((5•(x2))•y))(x•(y2)))(2Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyClick here👆to get an answer to your question ️ Solve (x^3 3xy^2) dx (y^3 3x^2y)dy = 0

X 9y 3xy X Y Answer It Plz With Full Maths Brainly In

If X Y 2 Then What Is The Value Of X Y 6xy Quora

Solution 1Show Solution Given f (x) = x 3 3xy 2 15x 2 15y 2 72x (1) STEP 1 for maxima, minima,` (delf)/ (delx)=0; We have (x3 y3) = 3xy2 dy dx We can rearrange this Differential Equation as follows 3 dy dx = x3 y3 xy2 = x3 xy2 y3 xy2 = x2 y2 y x = ( x y)2 y x This would lead us to try a substitution, Let v = y x ⇒ y = vxTypo/misspeak around 4 minutes 369=27Multivariable Calculus Find all local maxima/minima and saddle points for the function f(x,y) = x^3 3xy y^3 W

Solve The Factorise X3 9y3 3xy X Y Brainly In

X 3 Y 3 Z 3 Novocom Top

Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and 0 Follow 0 A K Daya Sir, added an answer, on 25/9/13 A K Daya Sir answered this x 3 y 3 = (x y) (x 2 xy y 2 ) this formula can be derived from (x y) 3 = x 3 y 3 3xy (x y) x 3 y 3 = (x y) 3 3xy (x y) x 3 y 3 = (x y) (x y) 2 3xy = (x y) x 2 y 2 2xy 3xy = (x y) (x 2 xy y 2 ) Was this answerQuestion The equation x3 3xy y3 = 1 is solved in integers Find the possible values of xy Found 3 solutions by Alan3354, Edwin McCravy, richard1234

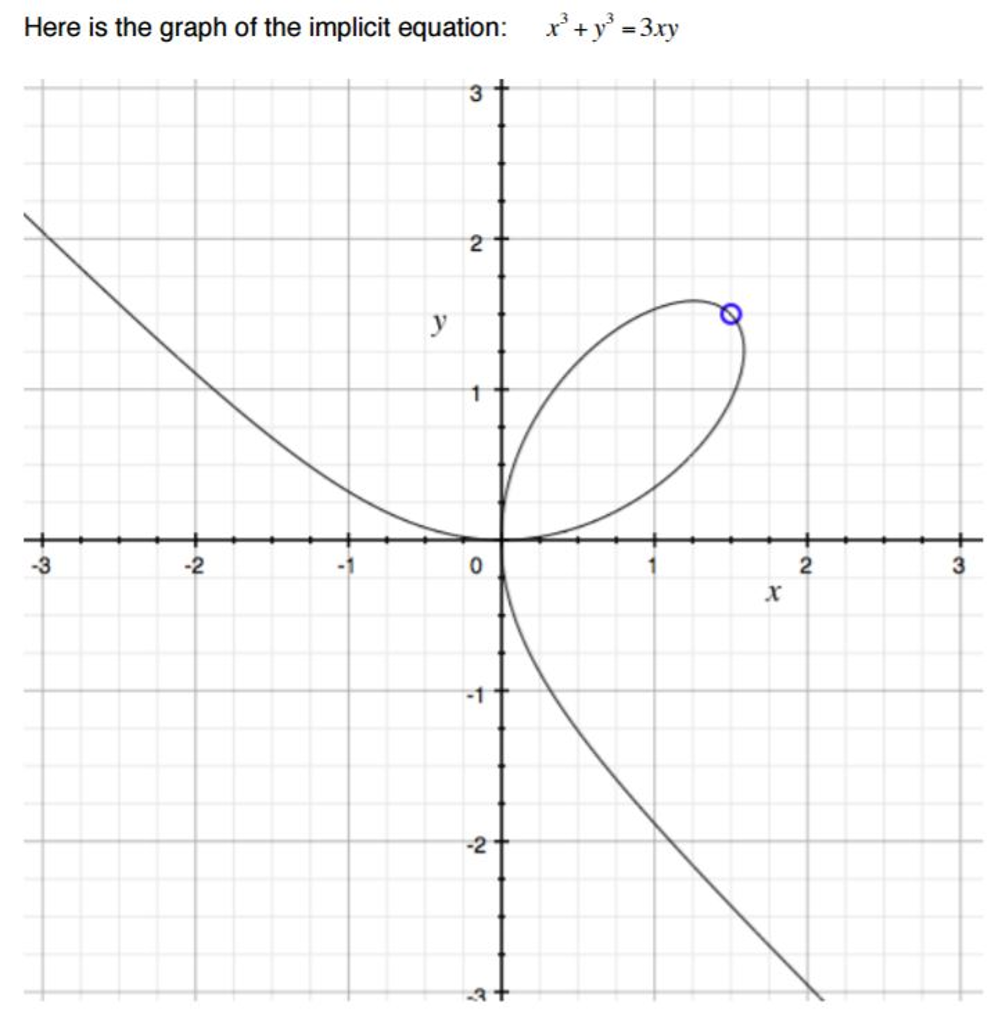
Here Is The Graph Of The Implicit Equation X 3 Y 3 Chegg Com

Algebraic Identities

 The solution of the differential equation (3xy y^2)dx (x^2 xy)dy = 0 is (A) x^2(2xy y^2) = c^2 asked in Differential equations by AmanYadav ( 556k points) differential equationsHow do I solve the general solution of (x^3y^3) dx xy^2dy = 0?Simplifying 3(X y) = y (X * 3 y * 3) = y (3X 3y) = y Solving 3X 3y = y Solving for variable 'X' Move all terms containing X to the left, all other terms to the right Add '3y' to each side of the equation 3X 3y 3y = y 3y Combine like terms 3y 3y = 0 3X 0 = y 3y 3X = y 3y Combine like terms y 3y = 2y 3X = 2y Divide each side by '3'

A X3 Y2 B X2 Y3 C X3 Y3 D See How To Solve It At Qanda

Answers

Elaborating x 3 y 3 using identity a 3 b 3 = (a b) (a 2 ab b 2 ) = x ( x y) (x 2 xy y 2 ) 3xy (x y ) Taking common x ( x y ) in both the terms = x ( x y) {x 2 xy y 2 3y} ∴ x (x 3 y 3 ) 3xy ( x y) = x ( x y ) (x 2 xy y 2 3y) Concept Algebraic Expressions Report ErrorFind dy/dx x^3y^36xy=0 Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate Tap for more steps By the Sum Rule, the derivative of with respect to is Differentiate using the Power Rule which states that is whereReduce the greatest common factor on both sides of the equation x 3 \times 3 = 6 Rearrange unknown terms to the left side of the equation x = 6 3 \times 3 Calculate the first two terms x = 6 9 Calculate the first two terms x = 3 Write the solution set of the equations \begin{equation}\begin{cases}x = 3\\y = 3\end{cases}\end{equation}

X 9y 3xy X Y Answer It Plz With Full Maths Brainly In

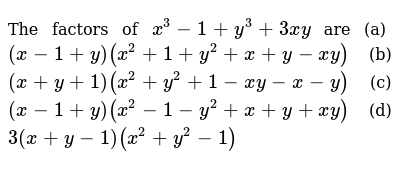
The Factors Of X 3 1 Y 3 3x Y Are A X 1 Y X 2 1 Y 2 X Y

 We need to differentiate x 3 y 3 ( x) = 3 x y ( x) Let's do each term one by one Differentiate x 3 You should quickly see this is 3 x 2 To differentiate ( y ( x)) 3, we need to remember the chain rule This can be written in many different ways, but this is a composition of the functions ( ⋅) 3 ∘ y ∘ xSolve for x Use the distributive property to multiply xy by x^ {2}xyy^ {2} and combine like terms Use the distributive property to multiply x y by x 2 − x y y 2 and combine like terms Subtract x^ {3} from both sides Subtract x 3 from both sides Combine x^ {3} and x^ {3} to get 0 Combine x 3 and − x 3 to get 0

3 A Find All Asymptotes Of See How To Solve It At Qanda

Q 2 Identify The Order And Degree Of The Following Chegg Com

How To Know At A Glance That Math X 3 3xy 2 2y 3 Math Is Factorable Quora

The Solution Of X Y 3 Dx 3xy 2 Dy 0 Is

Verify X Y 3 X3 Y3 3xy X Y Brainly In

Expand X X Y 3 3xy X Y

Find The Extreme Values Of The Function X 3 Y 3 3xy Sarthaks Econnect Largest Online Education Community

Factorise X X3 Y3 3xy X Y Brainly In

If A Line Y 3 X Cuts The Curve X 3 Y 3 3xy 5x 2 3y 2 4x 5y 1 0 At The Points A B And C

The Factors Of X 3 1 Y 3 3x Y Are A X 1 Y X 2 1 Y 2 X Y

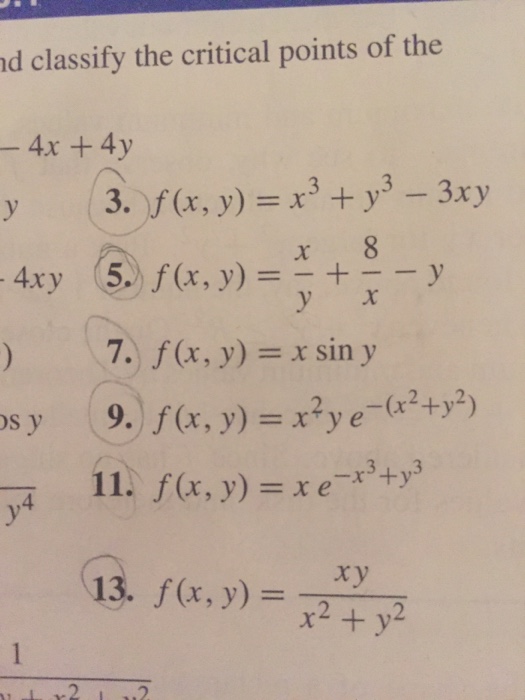
D Classify The Critical Points Of The 4x 4y Y 4m Chegg Com

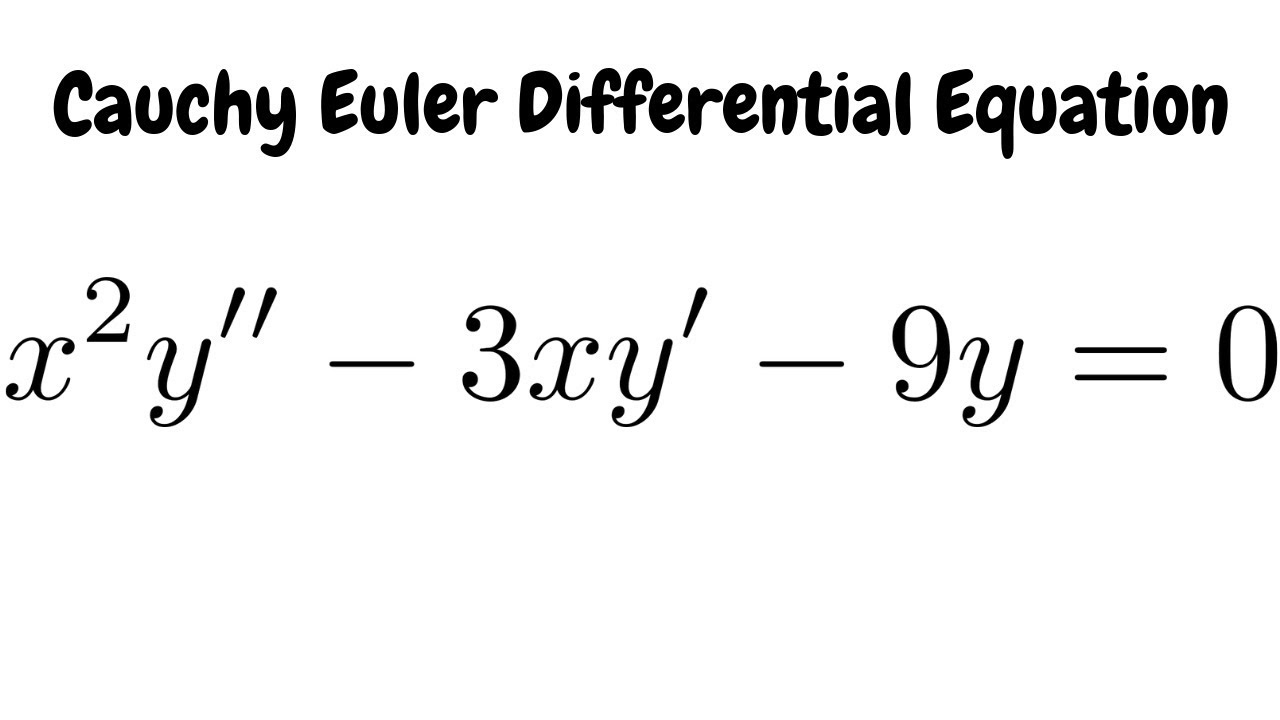
Solve X 2y 3xy 9y 0 Cauchy Euler Differential Equation Youtube

1

Consider The Function F X Y X 3 Y 3 3xy Chegg Com

If X 3 Y 2 3xy X Y Then Log X Y 3

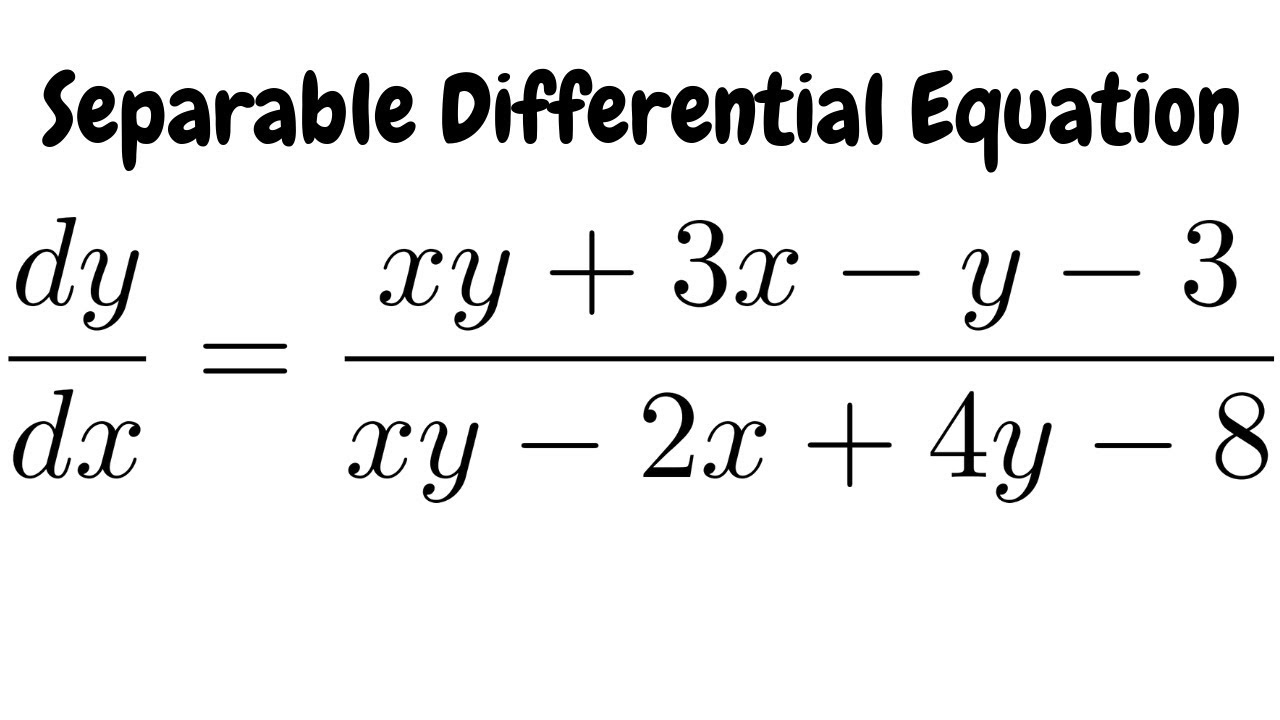
Separable Differential Equation Dy Dx Xy 3x Y 3 Xy 2x 4y 8 Youtube

How To Solve 3xy Y 2 Dx X 2 Xy Dy 0 Also I Wish To Knw When To Use Y Vx Or X Vy Mathematics Topperlearning Com H9faf2xx

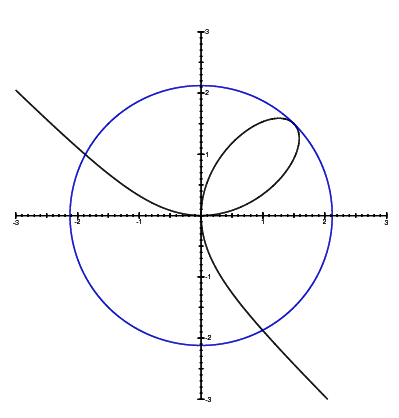
Relplot Equation Plotter

Ppt Polynomials Powerpoint Presentation Free Download Id

How To Solve Math Xy 2 Dy X 3 Y 3 Dx 0 Math Quora

Y Xyz 2x2y2z22xy2yz2zx See How To Solve It At Qanda

Solve The Exact Differential Equation X 3 Y 3 Dx Chegg Com

X Y 3 X3 Y3 3xy X Y Brainly In

Dx 1 Consider The Implicit Equation X3 Y3 3xy Chegg Com

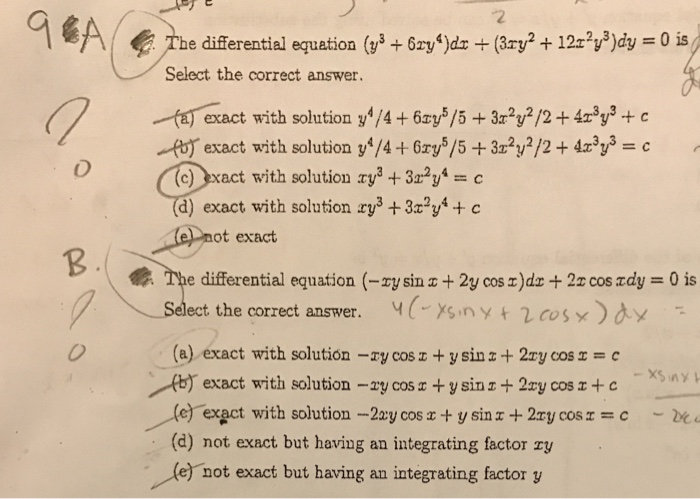
The Differential Equation Y 3 6xy 4 Dx 3xy 2 Chegg Com

If X 3 Y 2 3xy X Y Then Log X Y 3

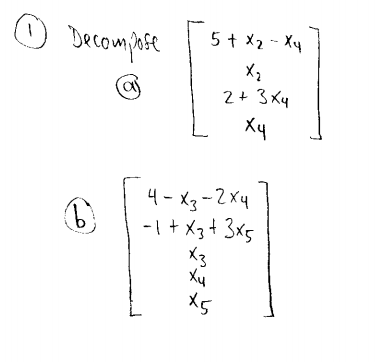
Answered Decompse 5 X2 Xy 2 3xy Xy 4 X3 Bartleby

Solve Differential Equation X 3 3xy 2 Dx Y 3 3x 2y Dy Maths Differential Equations Meritnation Com

Solve X 3 3xy 2 Dx Y 3 3x 2y Dy Sarthaks Econnect Largest Online Education Community

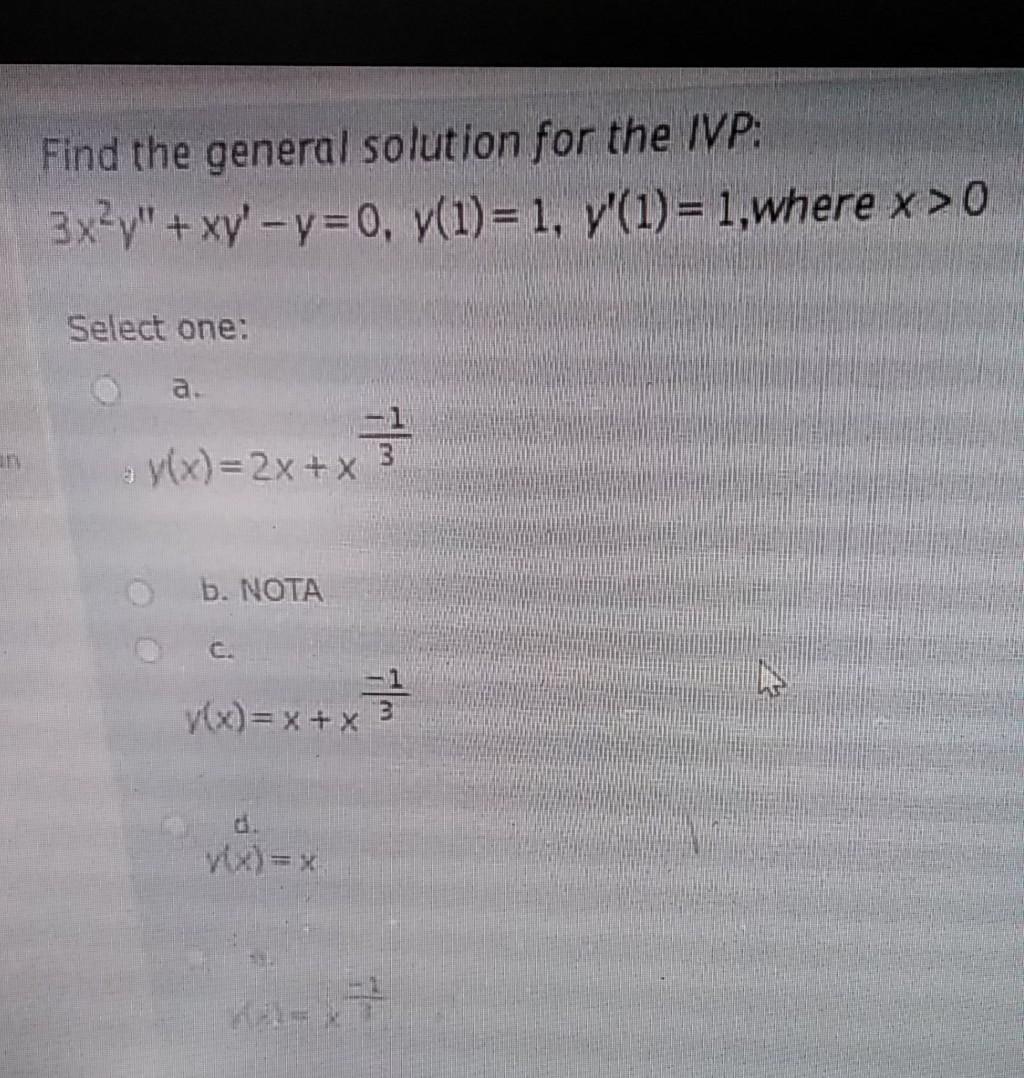
Find The General Solution For The Ivp 3xy Xy Y Chegg Com

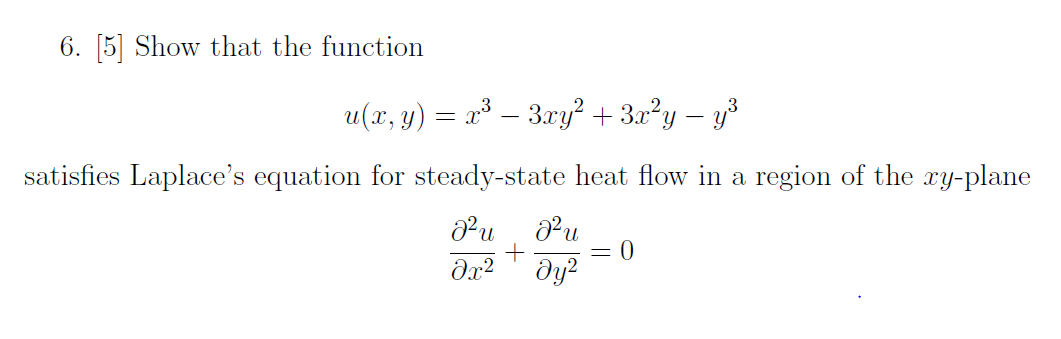
Show That The Function U X Y X 3 3xy 2 3x 2y Chegg Com

Y3 3xy2 X3 3x2y Find Dy Dx Plzzzzzzzzzzz Slove Ths As Fast As Possible Maths Continuity And Differentiability Meritnation Com

How To Evaluate Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube

Factorise X Y 3 X 3 Y 3 3xy X Y Brainly In

X 3 3xy 2 Dx Y 3 3x 2y Dy Youtube

Find All Values Of X Y Where Theorem 3 1 1 The Chegg Com

Factorise X3 9y3 3xy X Y Brainly In

If X 3 Y 2 3xy X Y Then Log X Y 3

Www Assignmentexpert Com Homework Answers Mathematics Answer Pdf

Tinkutara Equation Editor Math Forum Question

Find Du Dx When U Xlogxy Where X 3 Y 3 3xy 1 Brainly In

How To Draw The Graph Of X 3 Y 3 3xy Quora

X Y 3 X3 Y3 3xy X Y Proof It Maths Polynomials Meritnation Com

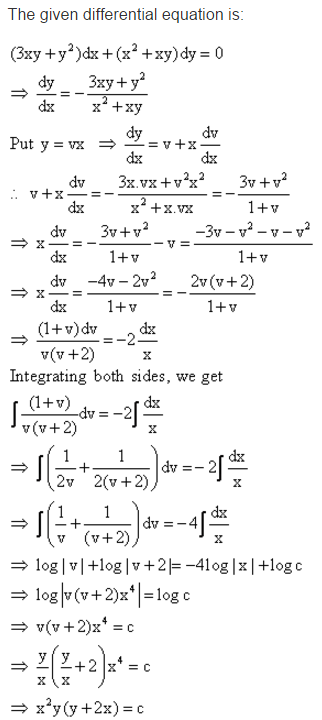
Find The Particular Solution Of Given Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 At X 1 Y 1 Mathematics Topperlearning Com D1ksg633

Second Partials Test For F X Y X 3 3xy Y 3 Youtube

X X 3 Y 3 3xy X Y

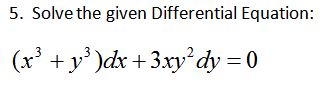
Solve The Given Differential Equation X 3 Y 3 Dx Chegg Com

Ex 12 2 4 A What Should Be Added To X 2 Xy Y 2 To Obtain

Differentiate X 2 Y 2 3xy 1 Youtube

Prove That X2 Y2 C X2 Y2 2 Is The General Solution Of The Differential Equation X3 3xy2 Dx Y3 3x2y Dy Where C Is Parameter Mathematics Shaalaa Com

X Y 3 X 3 Y 3 3xy X Y Verify Maths Meritnation Com

Solve Dy Dx 3xy Xy 3 30 Dy Dx X 2y 3 2x Chegg Com

How To Solve The General Solution Of X 3 Y 3 Dx Xy 2dy 0 Quora

Algebraic Expressions

If X 3 3xy 2 14 Y 3 3yx 2 13 And X Y Are Real Find The Maths Polynomials Meritnation Com

What Should Be Added To X2 Xy Y2 To Obtain 2x2 3xy Algebraic Expressions Maths Class 7

The Two Curves X 3 3xy 2 2 0 And 3x 2y Y 3 2 0 Youtube

3 A Classify Each Ode By Order And Linearity Y 3xy Xy 0 Homeworklib

If 5 X Y 2 121 R Mmd The Val 6 If X Y 7 And Xy 1 Gauthmath

If Math X 3 Y 3 3xy 1 Math What Is The Minimum Value Of Math X 2 Y 2 Math Quora

How To Factorise Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube

Statement 1 The Equation X 3 Y 3 3xy 1 Represents The Combine

If X 3 Y 3 1 3xy Where X Y Determine The Value Of X Y 1

If X 3 Y 3 9 And X Y 3 Then What Is The Value Of X 4 Y 4 Quora

Find Dydx Where X 3 Y 3 3xy 7

Transform X 3 Y 3 3xy 0 Mathematics Stack Exchange

Solve The Equation X 2 3xy Y 2 Dx X 2dy 0 Given That Y 0 And X 1

1

K 6y Y 1 7y 7y M 3x 4x N 6x X 0 2y 5 Gauthmath

X 3 3x 2 X 3 Factorise Novocom Top

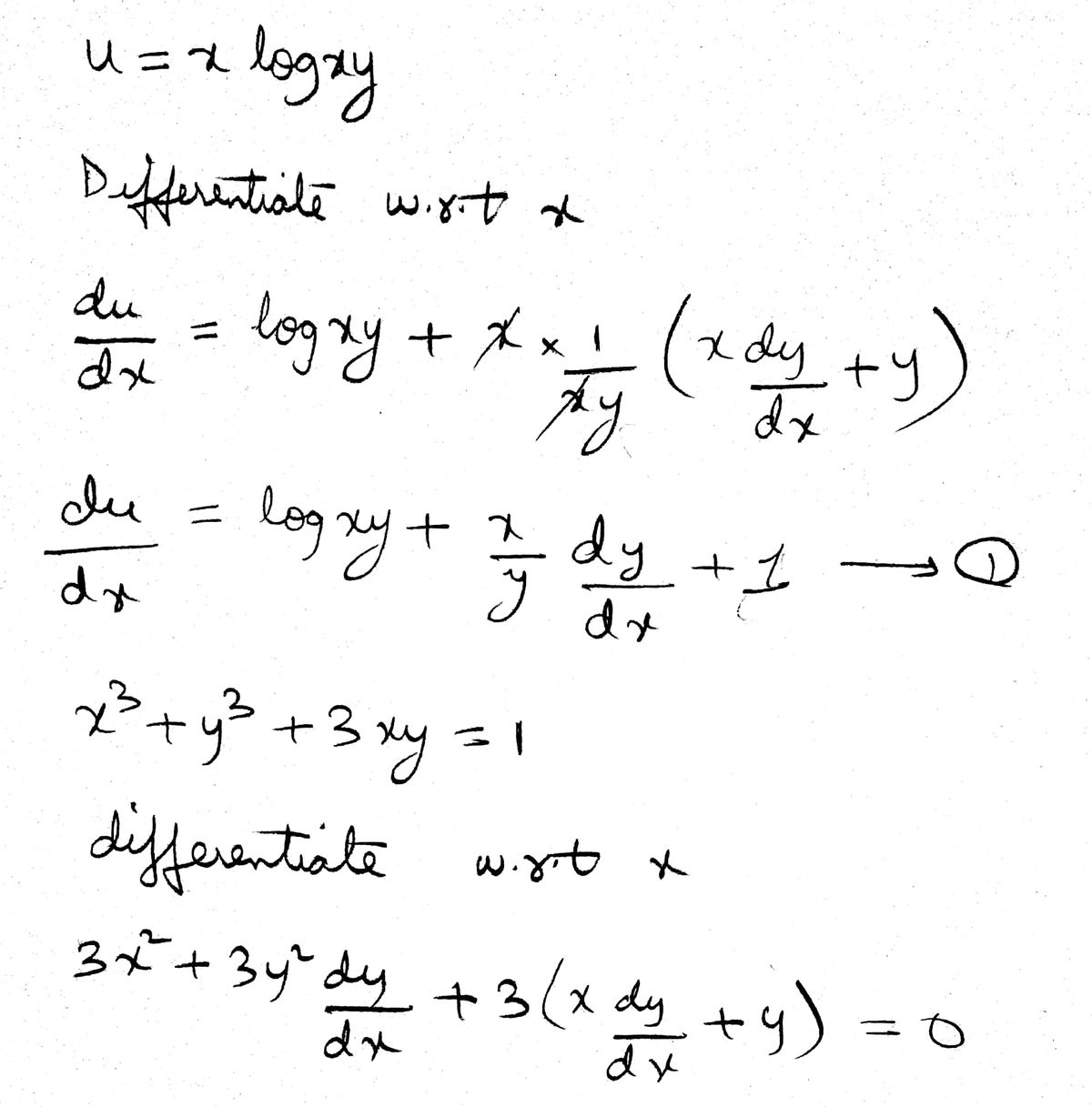
Answered If U X Log Xy Where X3 Y3 3xy 1 Find Bartleby

Let F X Y X 3 3xy 2 2y 3 Show That The Chegg Com

X3 9y3 3xy X Y এর উৎপ দক ব শ ল ষণ কর Brainly In

Factorize X X 3 Y 3 3xy X Y Sarthaks Econnect Largest Online Education Community

X X3 Y3 3xy X Y Maths Polynomials Meritnation Com

If X Y 12 And Xy 27 Then Find The Value Of X3 Y3 Polynomials Maths Class 9

Polynomials Ppt Video Online Download

Verify The Following Identity X Y 3 X3 Y3 3xy X Y Brainly In

K 6y Y 1 7y 7y Jndei M 3x 4x N 6x X Je Gauthmath

How To Solve X 3 3xy 2 Dx 3x 2y Y 3 Dy Quora

Incoming Term: x(x^3-y^3)+3xy(x-y) solution,