A level curve is simply a cross section of the graph of z = f (x, y) taken at a constant value, say z = c A function has many level curves, as one obtains a different level curve for each value of c in the range of f (x, y)Highlight Specific Contour Levels This example shows how to highlight contours at particular levels Run the command by entering it in the MATLAB Command Window Web browsers do not support MATLAB commands Choose a web site to get translated content where available and see local events and offersLevel curves The two main ways to visualize functions of two variables is via graphs and level curves Both were introduced in an earlier learning module For your convenience, that learning module page is reproduced here
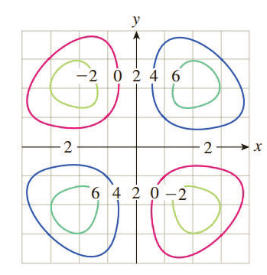
Exercises 55 58 Refer To The Following Plot Of Some Level Curves Of F X Y C For C 2 0 2 4
Level curves and gradients
Level curves and gradients-A level curve of a function is curve of points where function have constant values,level curve is simply a cross section of graph of function when equated to some constant values,example a function of two variables say x and y,then level curve is the curve of points (x,y),where function have constant valueCan be better understood by an exampleLevel curves Scroll down to the bottom to view the interactive graph A level curve of f (x, y) is a curve on the domain that satisfies f (x, y) = k It can be viewed as the intersection of the surface z = f (x, y) and the horizontal plane z = k projected onto the domain




Level Curves Of The Error After Iterations The Star Marks The Download Scientific Diagram
Level Curves Example 1 (Solution Strategy) Sketch some level curves of the function Solution First, let z be equal to k, to get f (x,y) = k Secondly, we get the level curves, or Notice that for k >0 describes a family of ellipses with semiaxes andLevel Curves A level curve is a slice through a surface When we have a surface described by {eq}z = f (x,y) {/eq}, level curves are the slice through planes of constant {eq}z = c {/eq}Free ebook http//tinyurlcom/EngMathYT How to sketch level curves and their relationship with surfaces Such ideas are seen in university mathematics and
Original question Find an equation of the level curve of f(x,y) = yx^2 – y^2 through the point (2,1) and find an equation of the tangent line to the level curve at this point I think I have found the equation of the tangent line to the level curve 10 = 4x 2y (is this correct??), but I have no idea how to find the equation of the level curveGradient is perpendicular to the level curves) Note, this problem is strictly about 2D functions w = f(x, y) and their gradients and level curves Also note, for Answer Suppose w = f(x, y) and we have a level curve f(x, y) = c Implicitly this gives a29 Exact Equations and Level Curves 151 29 Exact Equations and Level Curves A level curve or a conservation law is an equation of the form U(x;y) = c Hikers like to think of Uas the altitude at position (x;y) on the map and U(x;y) = cas the curve which represents the easiest walking path, that is, altitude does not change along that route
Level Curves Author Kristen Beck Topic Functions This worksheet illustrates the level curves of a function of two variables You may enter any function which is a polynomial in both andIf you're working with some other 3D graph then, you'll want to check to find which values of x and y together produce z The easiest way to do this is to set a fixed value for one variable and then solve for the other So, if you have a function F (x,y) = 2x 3y, and you want toSolution The level curves of are curves in the plane along which has a constant value We now sketch the resulting curves for a couple values of The curve consists of all points satisfying That is, it has points where or Similarly, the and level curves are given by and Hence our sketch of the level curves of looks like




Level Curves In Mathbb R 3 Mathematics Stack Exchange




Some Level Curves For The Total Energy E U V The Trajectory That Download Scientific Diagram
At Level The Curve, we aim to make everyday life easier for people by creating products that adapt to the customers' needs and wants, and at a low price The result is a consumeroriented approach which caters specifically to, as our name suggests, "leveling the curve" as well as the "playing field" for the disabled communityLevel curves of planes Prove that the level curves of the plane a x b y c z = d are parallel lines in the x y plane, provided a 2 b 2 ≠ 0 and c ≠ 0 Functions of Several Variables Graphs and Level Curves 0050 Calculus for Scientists and Engineers Early Transcendental Mathematica has a builtin command to generate plots of the level curves of a function f of two variables The basic form of the command is where F x, y is an expression in the variables x and y, which range over the respective intervals xmin, xmax and ymin, ymax For the function f with formula f (x, y) = , with x and y each
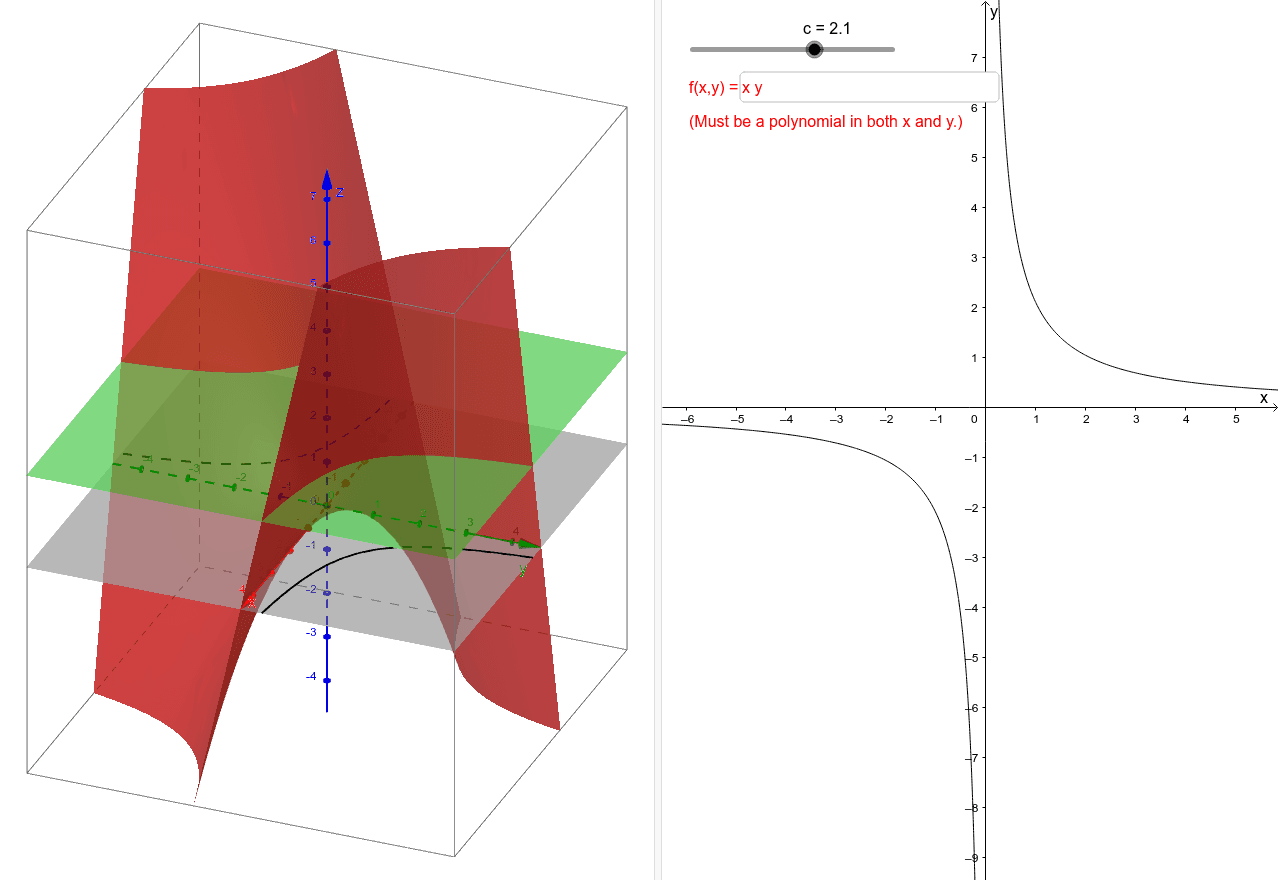



Level Curves Geogebra



Example Contour Plots Or Level Curves
curve direct Curve direct is a software intended for all people seeking to view the behavior of automatic breaking devices placed in cascade in a LV electrical network Curve direct is used to view coordination between devices This tool therefore enhances the level of continuity of service of an installationGet the free "Level Curves" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Mathematics widgets in WolframAlphaLevel Curve Grapher Level Curve Grapher Enter a function f (x,y) Enter a value of c Enter a value of c Enter a value of c Enter a value of c



Level Curves And Contour Plots Mathonline
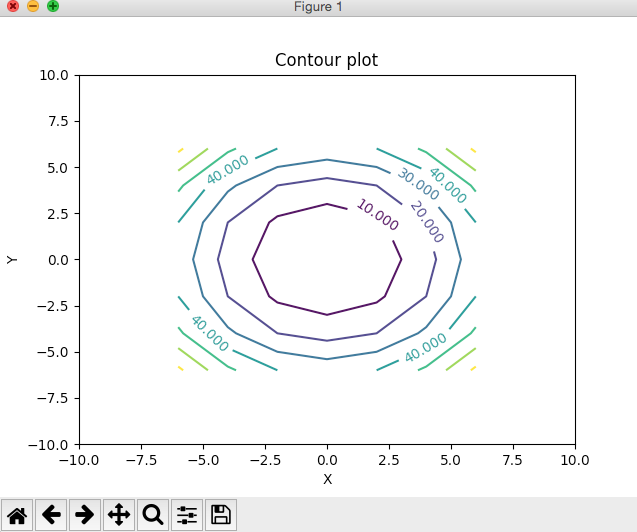



Contour Plot Using Python And Matplotlib Pythontic Com
The remaining finitely many level curves, corresponding to F (x, y, α i ), i = 1, , r, are also analyzed with the same strategyTherefore, the problem of determining the topology types of the level curves of S reduces to the computation of a critical level set Let us recall the results in (1) which allow to do thisLEVELS & CURVES is a onestop solution for all your digital marketing needs Our expertise conduct market research and this helps you to reach your exact target audience Being a leading digital marketing company we help you to reach a wider audience and reaching more audience we create more business opportunityGRADIENTS AND LEVEL CURVES There is a close relationship between level curves (also called contour curves or isolines) and the gradient vectors of a curve Indeed, the two are everywhere perpendicular This handout is going to explore the relationship between isolines and gradients to help us understand the shape of functions in
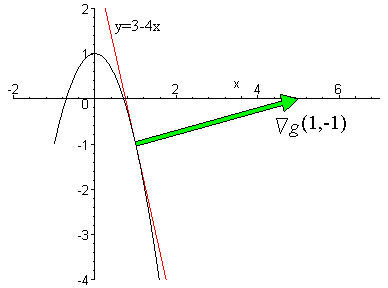



Gradients And Level Curves




A Few Level Curves Of Z F X Y Are Shown A As Accurately As You Can Approximate Bigtriangledown F 2 3 B Use Your Result From Part A To Obtain An Equation
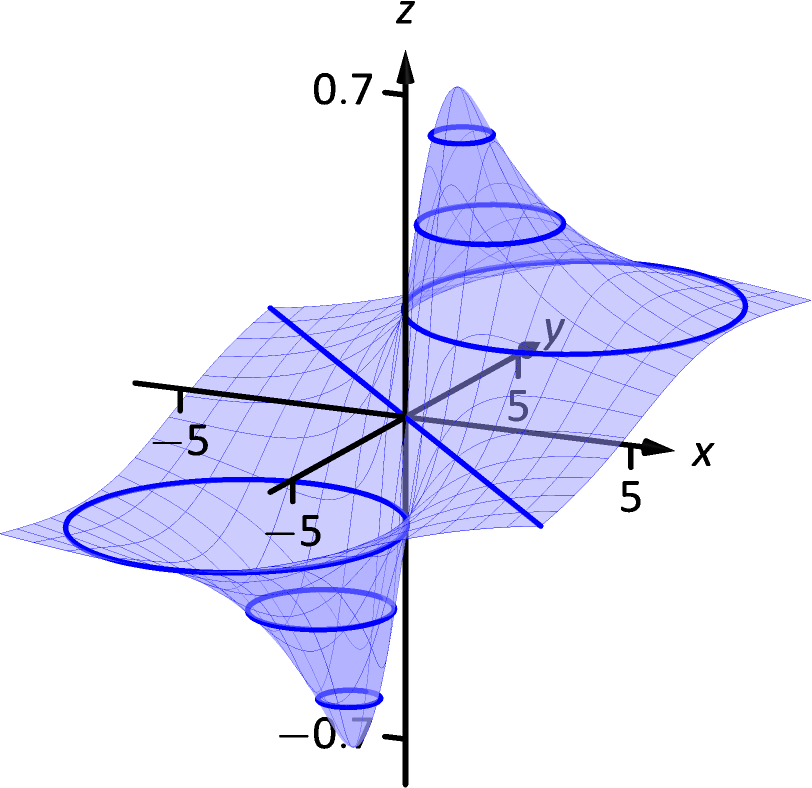
Level curves Loading level curves level curves Log InorSign Up x 2 y 2 − z 2 = 1 1 z = − 0 8 2 3Level curves Level Curves For a general function z = f(x, y), slicing horizontally is a particularly important idea Level curves for a function z = f(x, y) D ⊆ R2 → R the level curve of value c is the curve C in D ⊆ R2 on which fC = c Notice the critical difference between a level curve C of value c and the trace on the plane zSection 56 Level Surfaces Video Here is a short video about Level Surfaces in CalcPlot3D created by Professor Larry Green of Lake Tahoe Community College It is difficult to draw many interesting level surfaces by hand, but CalcPlot3D helps us explore them easily There are actually two ways to enter and graph the level surface equations for a particular function of three variables in




Session 35 Gradient Definition Perpendicular To Level Curves Part B Chain Rule Gradient And Directional Derivatives 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Exercises 55 58 Refer To The Following Plot Of Some Level Curves Of F X Y C For C 2 0 2 4
Like finding level curves for this $$ z=e^{x^2y^2}$$ Thanks in advance calculus graphingfunctions Share Cite Follow asked Nov 27 '14 at 53 João Pedro João Pedro 650 7 7 silver badges 23 23 bronze badges $\endgroup$ 2 Level Curve A level set in two dimensions Phase curves are sometimes also known as level curves (Tabor 19, p 14) SEE ALSO Contour Plot, Equipotential Curve, Level Surface, Phase Curve REFERENCES Tabor, M Chaos and Integrability in Nonlinear Dynamics An Introduction New York Wiley, 19From the definition of a level curve above, we see that a level curve is simply a curve of intersection between any plane parallel to the axis and the surface generated by the function




Level Curves Of The Error Function Download Scientific Diagram



Level Sets Ximera
A level curve of a function f (x,y) is a set of points (x,y) in the plane such that f (x,y)=c for a fixed value c Example 5 The level curves of f (x,y) = x 2 y 2 are curves of the form x 2 y 2 =c for different choices of c These are circles of radius square root of cExample 1 Let f ( x, y) = x 2 − y 2 We will study the level curves c = x 2 − y 2 First, look at the case c = 0 The level curve equation x 2 − y 2 = 0 factors to ( x − y) ( x y) = 0 This equation is satisfied if either y = x or y = − x Both these are equations for lines, so the level curve for c = 0 is two lines If youLevel Curves One of the most useful and common methods for visualizing functions (or surfaces) of two varibles is a Contour Map in which points of constant elevation are joined in a 2D plane to form level curves (or contour curves)



Level Curves Project Project




Level Sets Math Insight
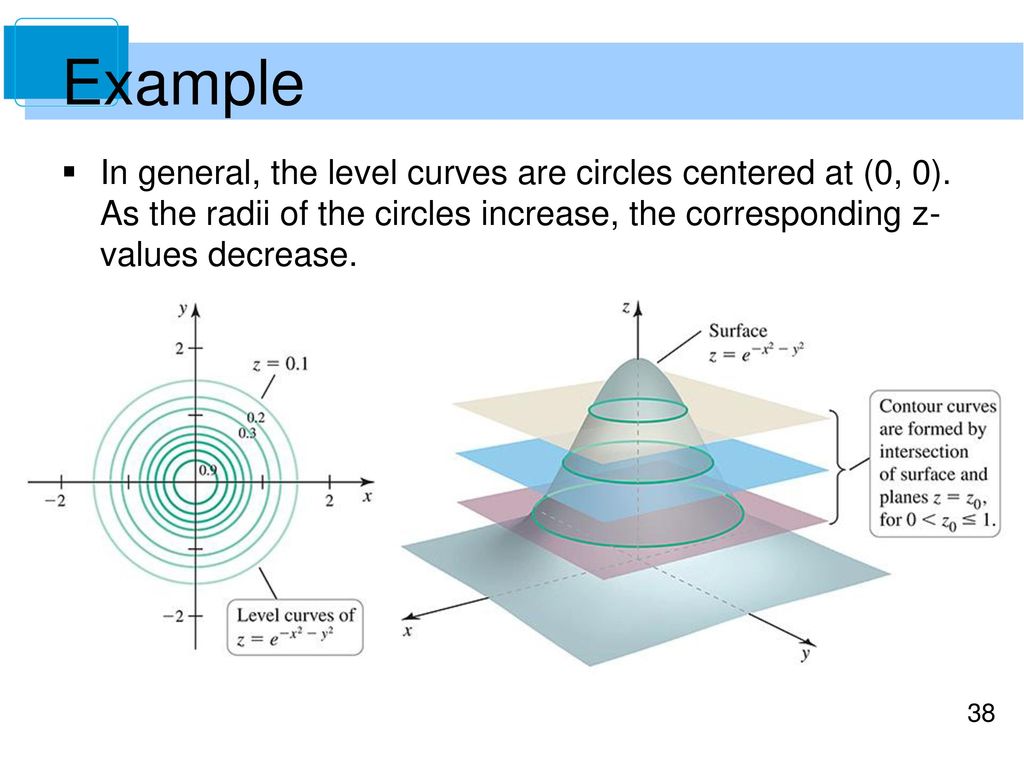
The level curves (or contour lines) of a surface are paths along which the values of z = f (x,y) are constant;Ie the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves The level curves of the function z = f (x,y) z = f (x, y) are two dimensional curves we get by setting z = k z = k, where k k is any number So the equations of the level curves are f




Level Curves Are Shown For A Function F Determine Whether The Following Partial Derivatives Are Positive Or Negative At The Point P A F X B F Y C F Xy Study Com




Level Sets Math Insight
Level curves and the implicit function theorem Differentiation The basic component of severalvariable calculus, twodimensional calculus is vital to mastery of the broader field This extensive treatment of the subject offers the advantage of a thorough integration of linear algebra and materials, which aids readers in the development of geometric intuitionFind 7 ways to say LEVEL CURVE, along with antonyms, related words, and example sentences at Thesauruscom, the world's most trusted free thesaurusThe level curves in this case are just going to be lines So, for instance, if we take the level curve at z equals 0, then we have just the equation 2x plus y equals 0 And so that has intercept so we're looking at so 0 equals 2x plus y, so that's just y equals minus 2x So that's this level curve




Gate Ese Level Curves And Surface Of A Function In Hindi Offered By Unacademy




Gradient And Level Curve Geogebra
A level curve of a function f(x,y) is the curve of points (x,y) where f(x,y) is some constant value A level curve is simply a cross section of the graph of z=f(x,y) taken at a constant value, say z=c A function has many level curves, as one obtains a different level curve for each value of c in the range of f(x,y)Level sets show up in many applications, often under different names For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an implicit equationAnalogously, a level surface is sometimes called an implicit surface or an isosurface The name isocontour is also used, which means a contour of Level curves Author Siamak The level curves of two functions and Blue represents and red represents Since and are both harmonic and is a harmonic conjugate of , the level curves of and intersect each other at right angles



Problem Of Level Curves Leading Lesson



13 1 Introduction To Multivariable Functions Chapter 13 Functions Of Several Variables Part Calculus Iii
Practice problems Sketch the level curves of Sketch the threedimensional surface and level curves of Consider the surface At , find a 3d tangent vector that points in the direction of steepest ascent Find a normal vector to the surface at the point Give the equation for the tangent plane to the surface at the pointThe latter curve is obviously ) (y^2)/b = z/c will result in a saddle shape or a hyperbolic paraboloid Basically, the crest, or bottom, of the level curve will be at (0,0,0) and there will a This will give us the sketch of level curves of the function In this video we're going to talk about how to find the level curves both graphically (by looking at a picture of the threedimensional figure) and algebraically, by replacing z in the multivariable function with a constant c, and then substituting different values for c in order to




Left Level Curves Of Distorted Density F X Y Center Level Download Scientific Diagram



Relief Functions And Level Curves
For example, for f(x,y) = 4x2 3y2 the level curves f = c are ellipses if c > 0 Level curves allow to visualize functions of two variables f(x,y) Example For f(x,y) = x2 − y2 the set x2 − y2 = 0 is the union of the lines x = y and x = −y The set x2 − y2 = 1 consists of two hyperbola with with their "noses" at the point



Relief Functions And Level Curves
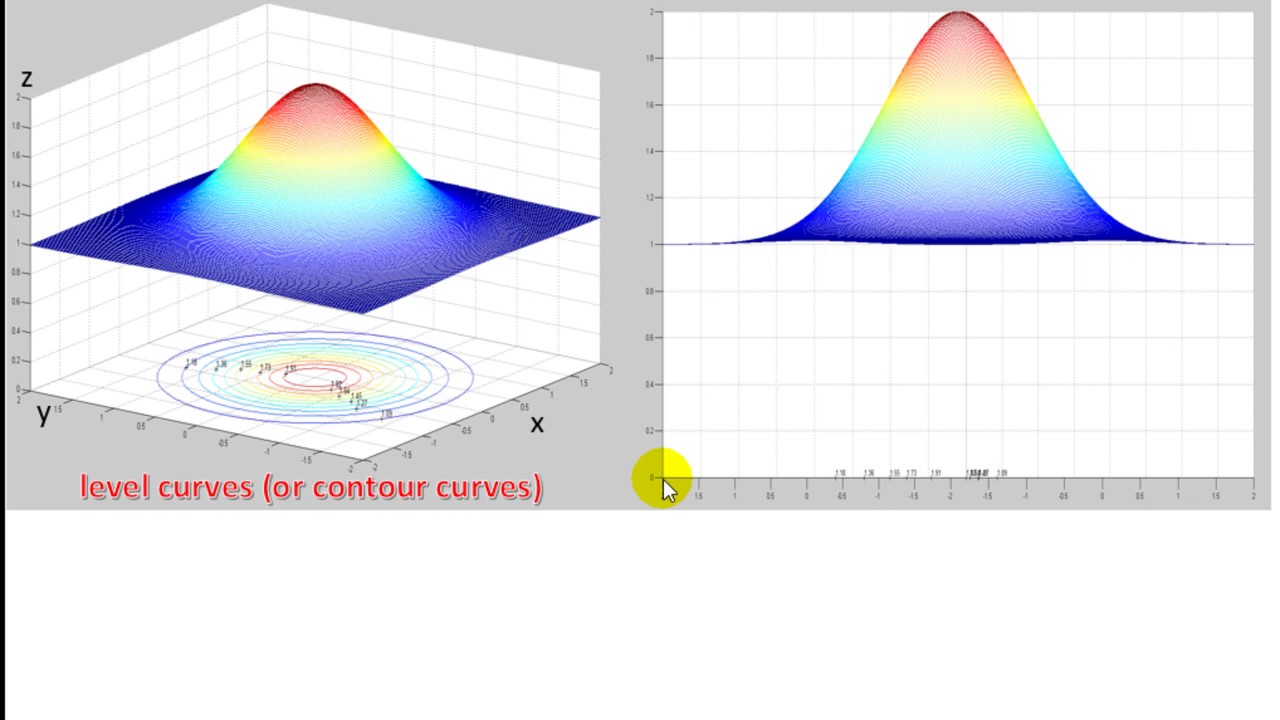



Level Curves Or Contour Curves Youtube




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Surface From Level Curves Of Unkown Levels In Matlab Stack Overflow




13 1 Functions Of Several Variables Mathematics Libretexts



1




Lesson 15 Gradients And Level Curves




Univ Vector Calculus Drawing A Contour Map With Level Curves Learnmath




What Does It Imply When Two Lines Cross Each Other In A Level Curve Mathematics Stack Exchange




Level Set Wikipedia




Level Curves




Matlab How Can I Get The Expression Of The Level Curves Of A Function Stack Overflow




Level Set Wikipedia




Calculus Iii Functions Of Several Variables




Relation Between Level Curves And Horizontal Traces Tex Latex Stack Exchange




Schematic Level Curves Of G P Q Values Of Wbow Kernel And The New Download Scientific Diagram




Level Curves Example 1



Introduction To Functions Of Several Variables Ppt Download




Level Sets Ximera



Contour Lines Rodolphe Vaillant S Homepage




Level Curves Of C R R Solid Lines Limiting Curve Labeled Zero Download Scientific Diagram
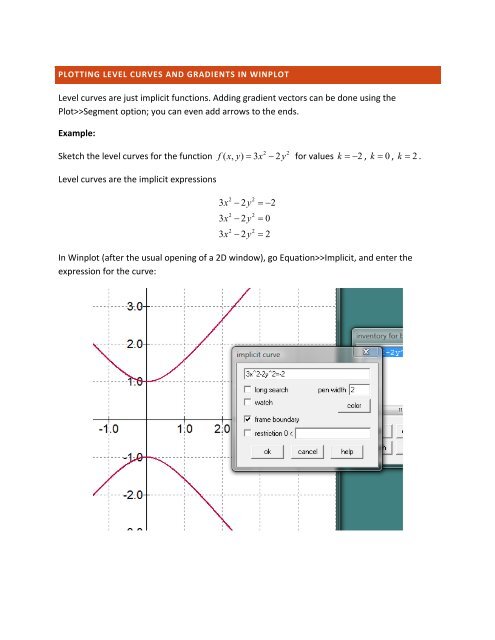



Level Curves And Gradient Vectors In Winplot




Lesson 15 Gradients And Level Curves




Session 35 Gradient Definition Perpendicular To Level Curves Part B Chain Rule Gradient And Directional Derivatives 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Visualizing Surface And Level Curves Youtube
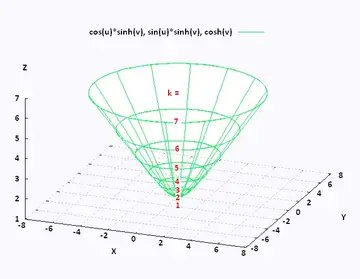



Mathematics Calculus Iii




Calculus Iii Functions Of Several Variables




Level Curves Curves Level Stvincent Glogster Edu Interactive Multimedia Posters




Level Curves Calcme Documentation Wiris




How To Find The Level Curves Of F X Y E 1 X 2 Y 2 Math Videos F X Curves




Level Curves




Problems With Level Curves First Steps Julialang




Contour Maps In Matlab




Level Curves Of Functions Of Two Variables Youtube




File Cubic Julia Set C 0 0 78 I With Internal Level Curves Png Wikimedia Commons




Level Set Wikipedia
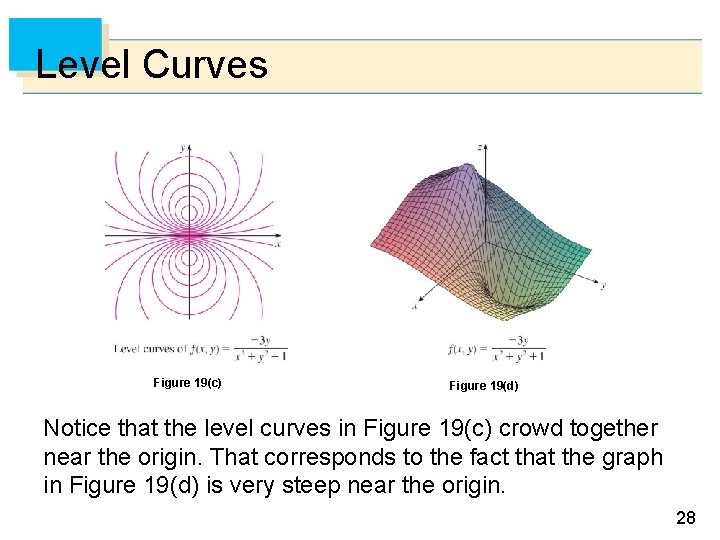



14 Partial Derivatives Copyright Cengage Learning All Rights



1
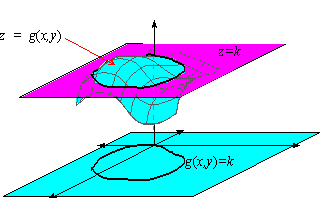



Gradients And Level Curves




Level Set Examples Math Insight



Http Math Oregonstate Edu Garity 254h Winter13 Notes 10 Graphs Levelcurves Pdf
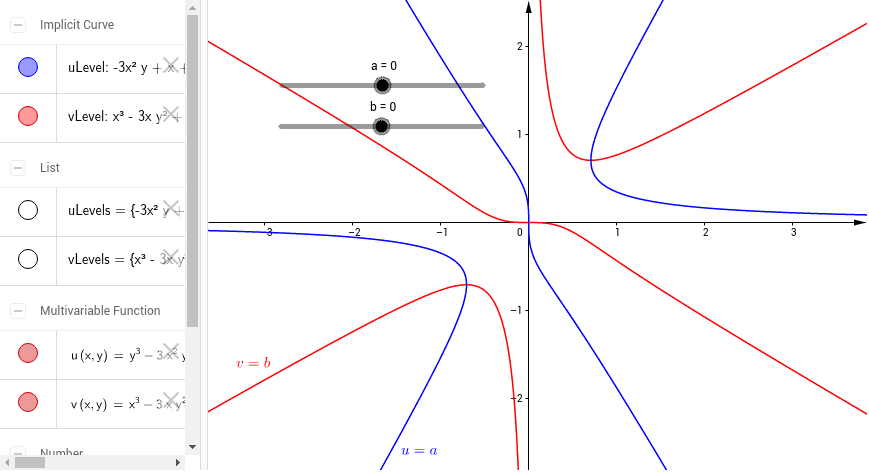



Level Curves Geogebra




16 1 Functions Of Several Variables




Level Curves Calculus



1




How To Sketch Level Curves Vector Calculus Vector Calculus Calculus Math Notes




Lecture Notes Chapter 1 1 Part2 Contourlines Level Curves And 3d Graphs Pdf




Level Curves And Implicit Differentiation Studocu



Http Academic Brcc Edu Ryanl Modules Multivariable Traces Traces Pdf
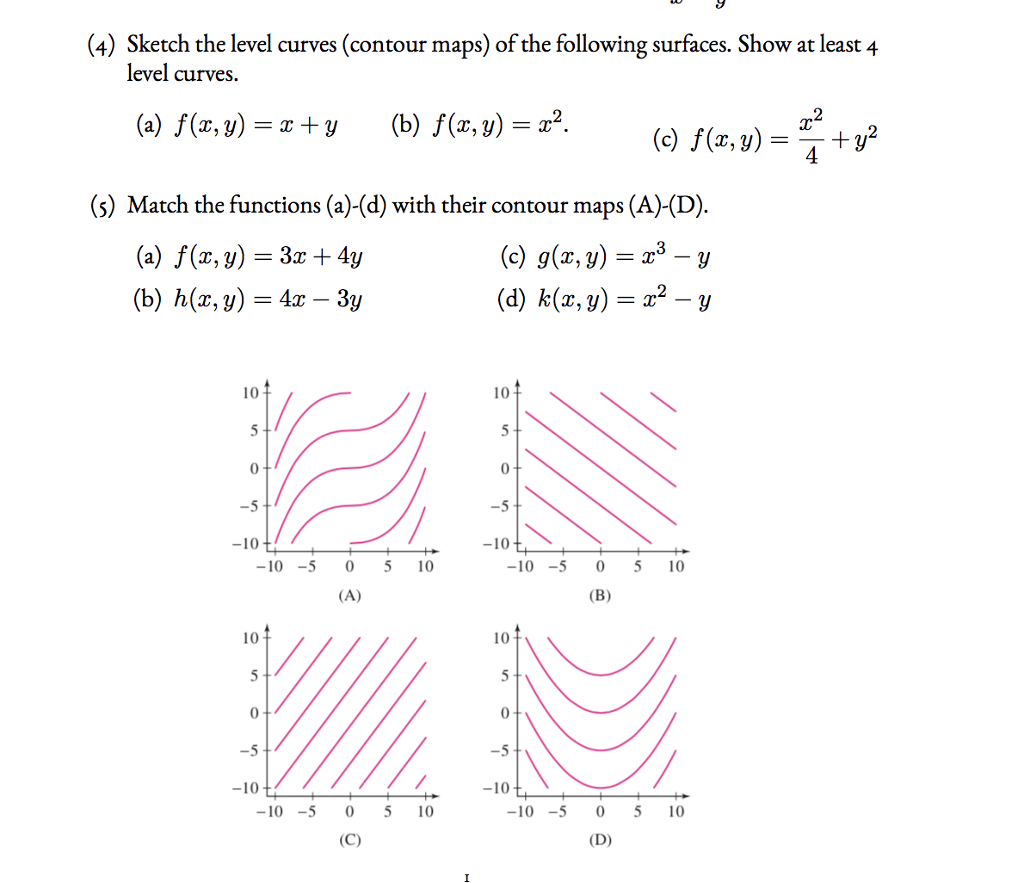



4 Sketch The Level Curves Contour Maps Of The Chegg Com




Level Curves Geogebra Dynamic Worksheet




Level Curves Of The Error After Iterations The Star Marks The Download Scientific Diagram



Contour Lines Rodolphe Vaillant S Homepage
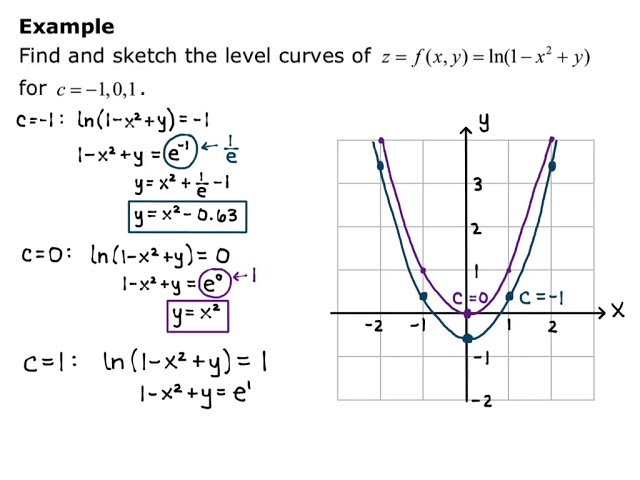



Section 13 1 Level Curves Youtube




Level Sets Math Insight




Math 2110 Section 13 1 Level Curves And Level Surfaces Youtube




Level Curve And A Surface Tex Latex Stack Exchange
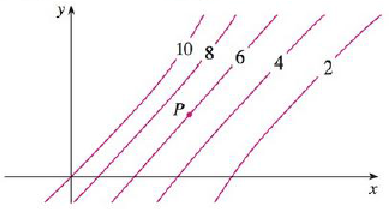



Level Curves Are Shown For A Function F Determine Whether The Following Partial Derivatives Are Positive Or Negative At The Point P A F X B F Y C F




Graphs And Level Curves
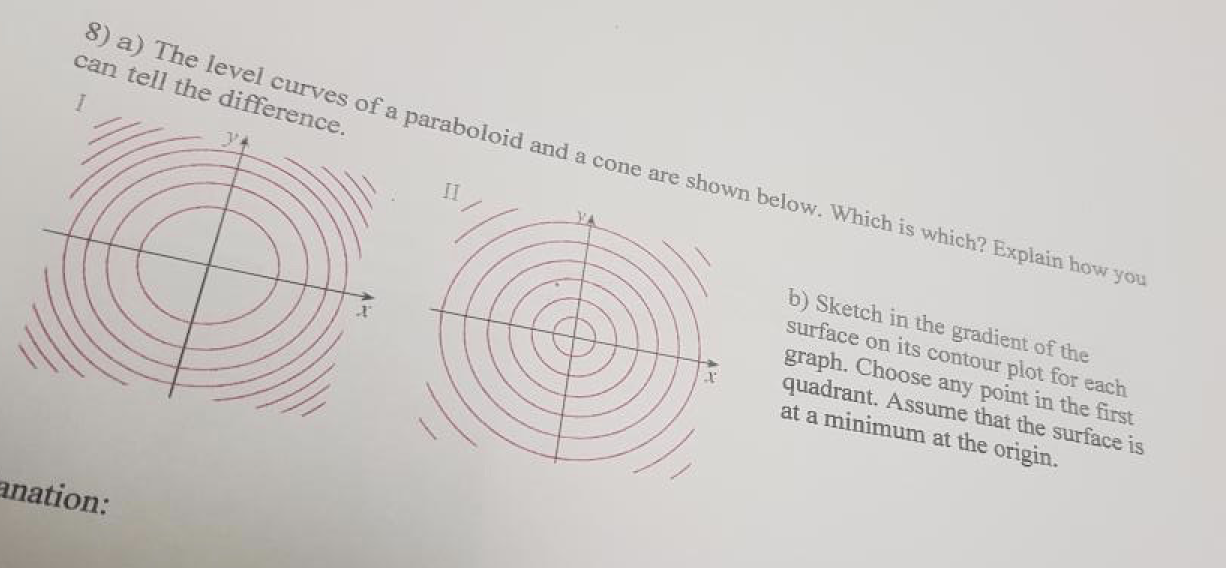



8 A The Level Curves Of A Paraboloid And A Cone Are Chegg Com



Demonstrates Plotting Contour Level Curves In 3d Matplotlib 3 4 2 Documentation




Level Curves Mit 18 02sc Multivariable Calculus Fall 10 Youtube



1




Level Curves Examples Level Surface
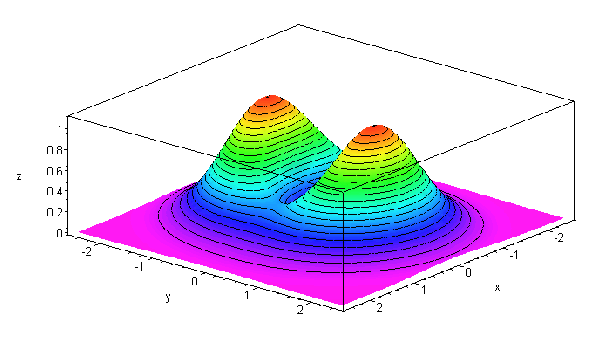



Level Curves
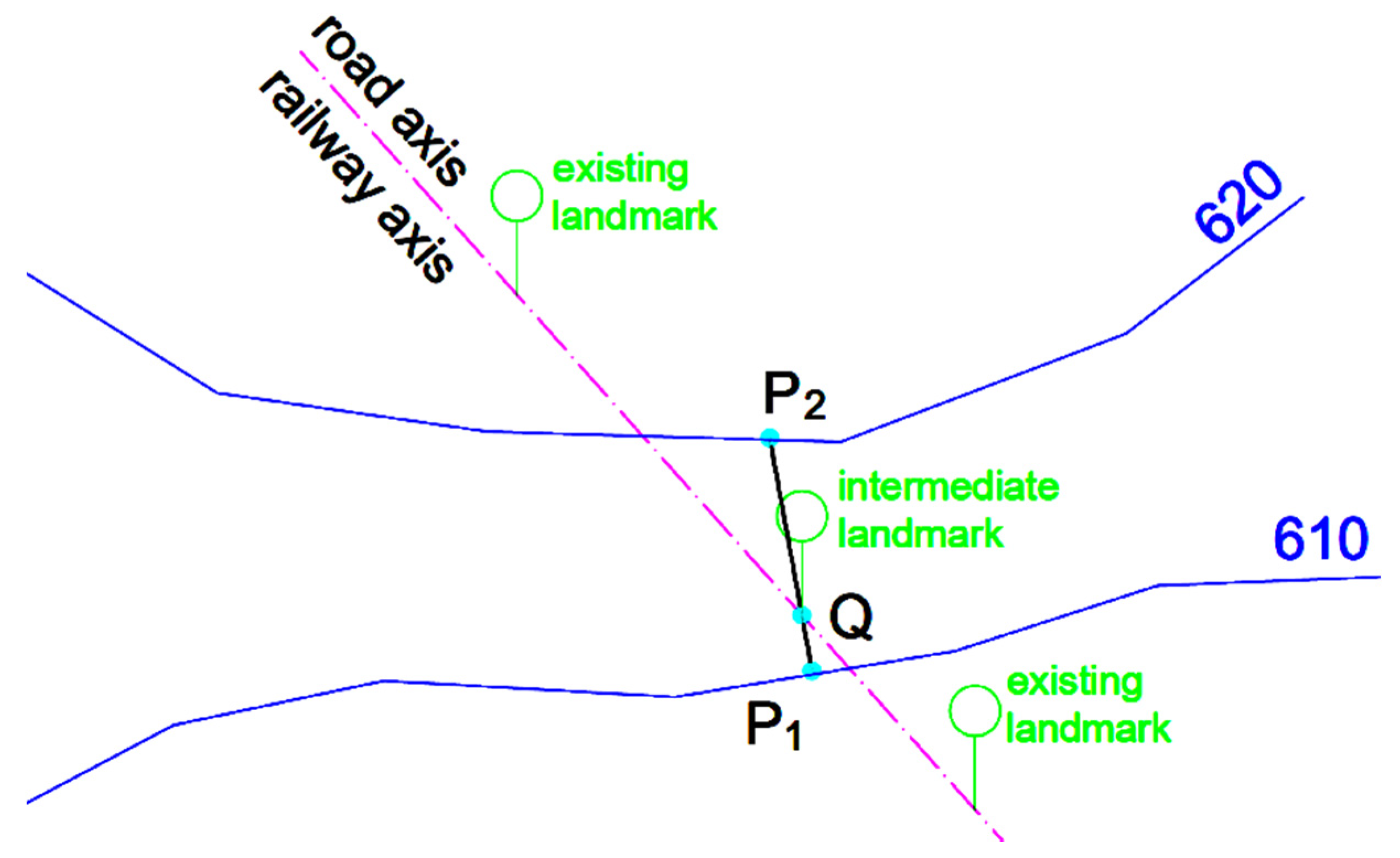



Applied Sciences Free Full Text Heuristic And Numerical Geometrical Methods For Estimating The Elevation And Slope At Points Using Level Curves Application For Embankments



Problem On Surfaces And Level Curves Leading Lesson




4 8 Pts The Level Curves Of Z F X Y Are Given Along Homeworklib



Level Curves




Level Curves




How To Sketch Level Curves Youtube
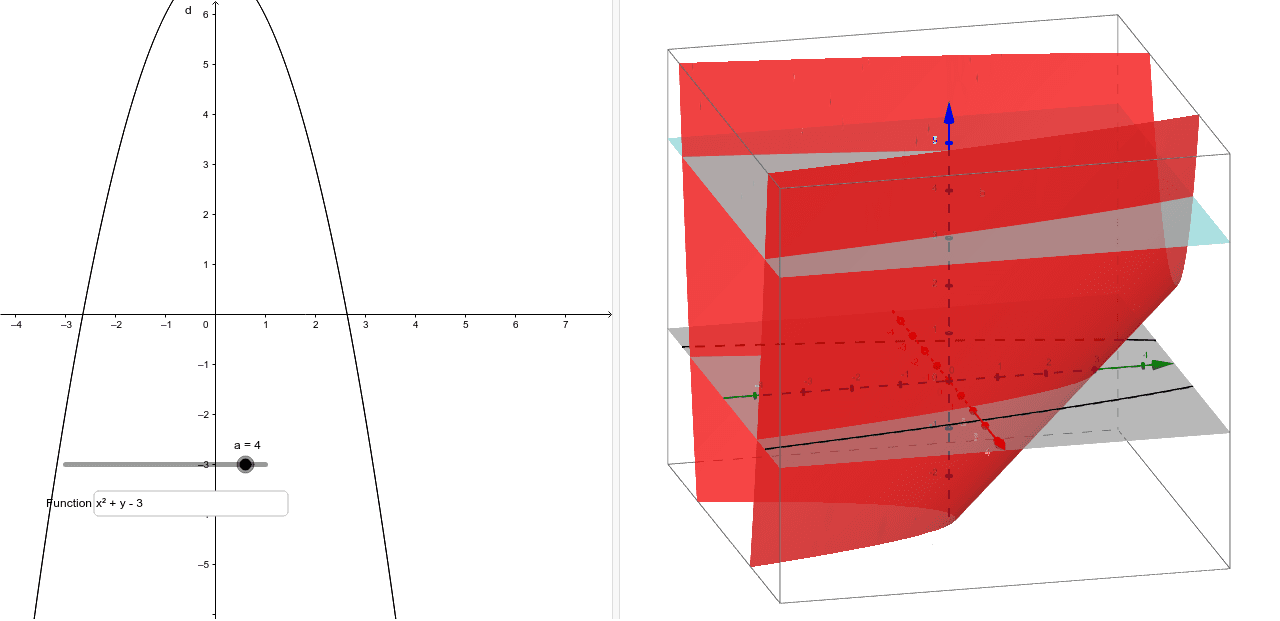



Visualizing Level Curves Geogebra




Describe The Level Curves Of The Function Z 8 2x 7y Chegg Com



Draw Level Curves For Functions Of Two Variables In C C Helper
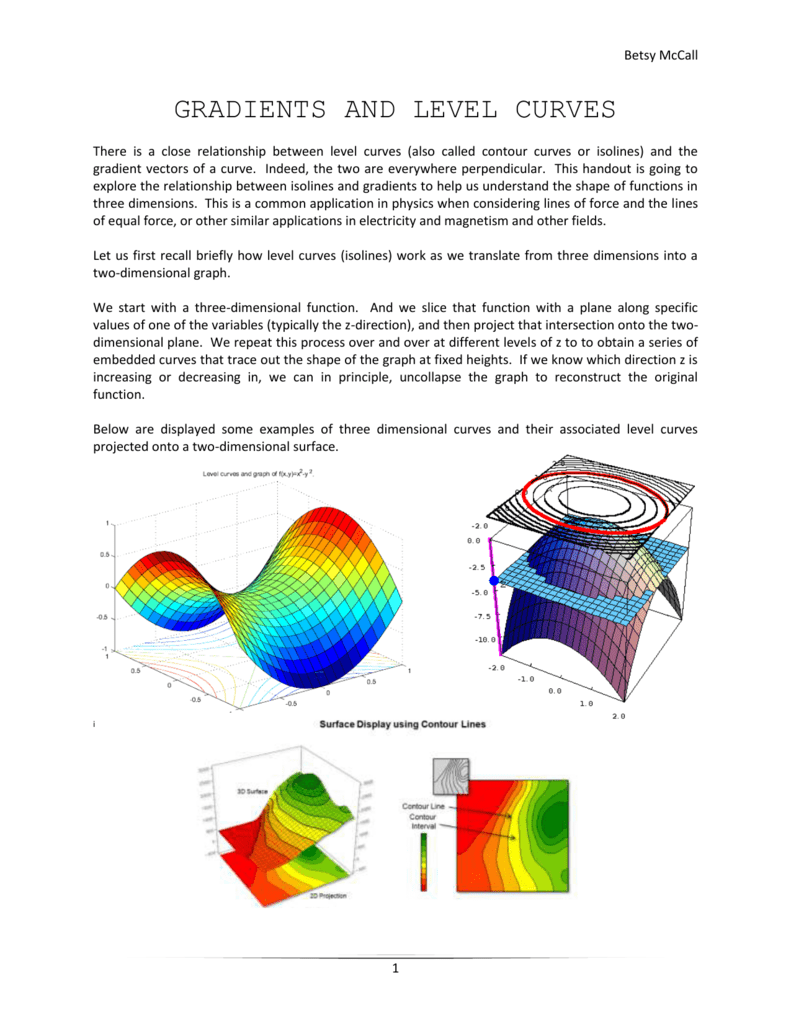



Gradients Level Curves




Level Curves Examples
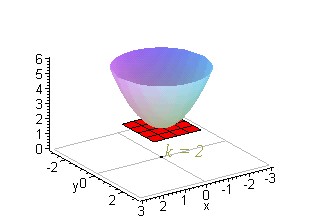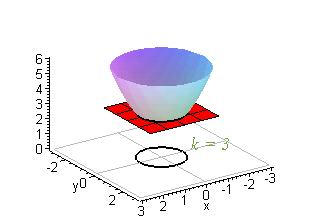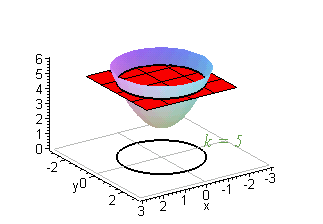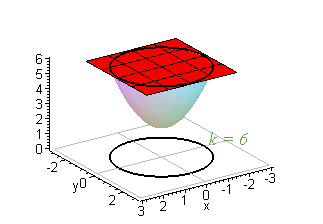



Gradients And Level Curves




Sketch The Level Curves Of The Function G X Y Chegg Com




Describe The Level Curves Of The Function Z X2 Chegg Com
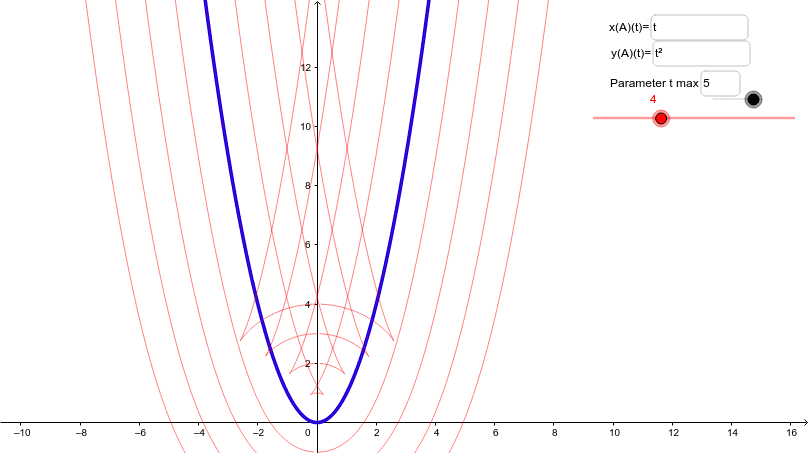



Level Curves Geogebra




How Can I Project Level Curves Onto The Axis Planes In 3d Usage Julialang




Level Set Examples Math Insight



0 件のコメント:
コメントを投稿